Leetcode Contest 189
Contents
Solved three out of four problems. Did not have enough time for the last problem.
Problem 1: leetcode 1450
# my solution
def busyStudent(self, startTime: List[int], endTime: List[int], queryTime: int) -> int:
n = len(startTime)
times = []
for i in range(n):
s, e = startTime[i], endTime[i]
times.append([s, 1])
times.append([e, -1])
times.sort(key = lambda x : (x[0], -x[1]))
count = 0
for tm in times:
if tm[0] < queryTime:
count += tm[1]
elif tm[0] == queryTime and tm[1] != -1:
count += tm[1]
else:
break
return count
This solution above is too complicated:
- no need to create a new
timeslist
Simply do
def busyStudent(self, startTime: List[int], endTime: List[int], queryTime: int) -> int:
count = 0
for i in range(len(startTime)):
if startTime[i] <= queryTime <= endTime[i]:
count += 1
return count
Problem 2: leetcode 1451
# my solution during contest
def arrangeWords(self, text: str) -> str:
words =[i.lower() for i in text.strip().split()]
if len(words) == 1:
return words[0][0].upper() + words[0][1:]
hist = {}
max_len = 0
for w in words:
if len(w) not in hist:
hist[len(w)] = []
hist[len(w)].append(w)
max_len = max(max_len, len(w))
res = []
for i in range(1, max_len + 1):
if i in hist:
res += hist[i]
head, tail = res[0], res[1:]
return " ".join([head[0].upper() + head[1:], " ".join(tail)])
Or if we do not want to use a bucket sort solution:
# this leverages Pyothon's soerted function to not move already sorted things around
def arrangeWords(self, text: str) -> str:
return " ".join(sorted(text.split(), key = len)).capitalize()
Problem 3: leetcode 1452
def peopleIndexes(self, fcs: List[List[str]]) -> List[int]:
n = len(fcs)
ans = []
for i in range(n):
is_contained = False
for j in range(n):
if j == i:
continue
s1 = set(fcs[i])
s2 = set(fcs[j])
if s1.issubset(s2):
is_contained = True
break
if not is_contained:
ans.append(i)
return ans
A python cleaner solution than mine:
# This is clean because
# A: create set only once
# B: using [for ... else clause][1] to save the use of a flag variable.
def peopleIndexes(self, favoriteCompanies: List[List[str]]) -> List[int]:
res = []
fc = [set(f) for f in favoriteCompanies] # A
N = len(fc)
for i in range(N):
for j in range(N):
if i != j and fc[i] & fc[j] == fc[i]: break # B
else:
res.append(i)
return res
This is a reference solution from
class Solution {
public:
// nice implementation for set contain
bool contain(const vector<string>& a, const vector<string>& b) {
if (a.size() < b.size()) return false;
int n = a.size(), m = b.size();
int i = 0, j = 0;
for (; j < m && i < n; ) {
if (a[i] == b[j]) {
++i; ++j;
} else {
++i;
}
}
return j == m;
}
vector<int> peopleIndexes(vector<vector<string>>& a) {
int n = a.size();
for (int i = 0; i < n; ++i) {
sort(a[i].begin(), a[i].end());
}
vector<int> ret;
for (int i = 0; i < n; ++i) {
bool found = false;
for (int j = 0; j < n; ++j) {
if (j == i) continue;
if (contain(a[j], a[i])) {
found = true;
break;
}
}
if (!found) ret.push_back(i);
}
return ret;
}
};
Problem 4 leetcode 1453
Brute Force
# O(N^3) solution
def get_circle(p, q):
# calculate circles with p, q on edge.
return [c1, c2]
def numPoints(points, r)
ans = 0
for i in range(n):
for j in range(n):
if i == j:
continue
if dist(p[i], p[j]) >= 2 * r + EPS:
continue
# get the two circles with point_i and point_j on the edge.
circles = get_circle(point[i], point[j])
for c in circles:
count = 0
for p in points:
if dist(p, c) <= r + EPS:
count += 1
ans = max(ans, count)
return ans
Angle Sweep 1
Looping through every point, draw a circle of radius r.
Pick a point A, If we draw circles for every other point to intersect with A, there are overlapping arc.
For example. The green arc is the overlap arc for circle A that touch both B and C. If I place one optimal circle’s center point on top of the green arc, the optimal circle will be able to cover all three points A, B, and C.
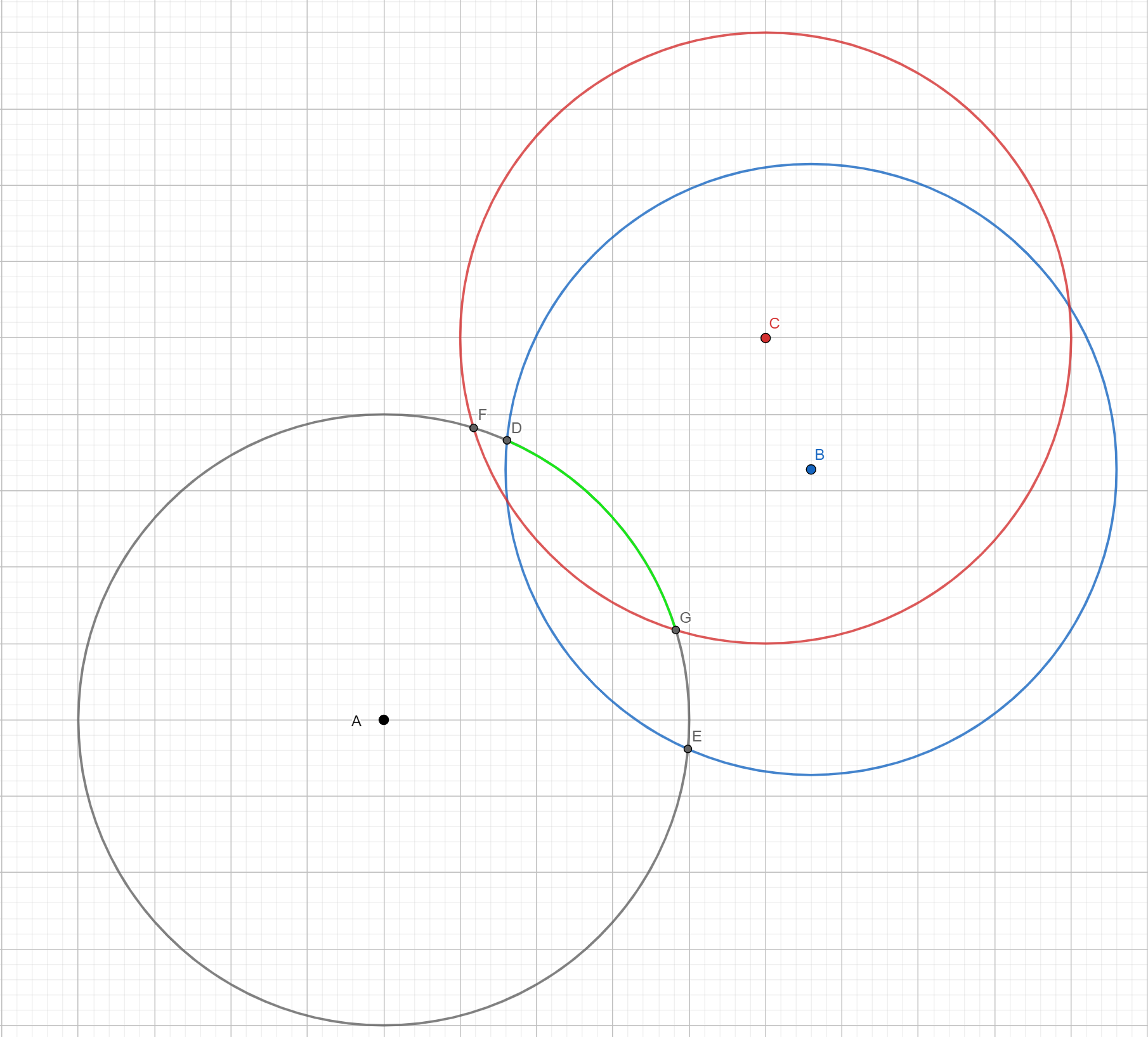
With the above observation, the answer is to find maximum overlapping segment count.
 link to the source geometry file
link to the source geometry file
# this soultion suffers from accuracy issue.
# [[5,5],[-2,5],[4,2],[1,-1],[1,1]]
# 5
# expect 5, but get 4
class Solution:
def dist(self, p1, p2):
dx = p1[0] - p2[0]
dy = p1[1] - p2[1]
return math.sqrt(dx ** 2 + dy ** 2)
def numPoints(self, points: List[List[int]], r: int) -> int:
n = len(points)
ans = 1
for i in range(n):
segments = []
for j in range(i + 1, n): # A: bug need to also consider pair(j, i)
A, B = points[i], points[j]
if self.dist(A, B) > 2 * r:
continue
mid_point = math.atan2(B[1] - A[1], B[0] - A[0])
half_arc = math.acos(self.dist(A, B)/2/r)
start = mid_point - half_arc
end = mid_point + half_arc
segments.append([start, 1])
segments.append([end, -1])
sorted_segments = sorted(segments, key = lambda x: (x[0], -x[1]))
# print(sorted_segments)
dart_count = 1
for segment in sorted_segments:
dart_count += segment[1]
ans = max(ans, dart_count)
return ans
# O(N^2 * logN)
class Solution:
def dist(self, p1, p2):
dx = p1[0] - p2[0]
dy = p1[1] - p2[1]
return math.sqrt(dx ** 2 + dy ** 2)
def numPoints(self, points: List[List[int]], r: int) -> int:
n = len(points)
ans = 1
for i in range(n):
segments = []
for j in range(n):
if i == j: # label A: bug fixed.
continue
A, B = points[i], points[j]
if self.dist(A, B) > 2 * r:
continue
mid_point = math.atan2(B[1] - A[1], B[0] - A[0])
half_arc = math.acos(self.dist(A, B)/2/r)
start = mid_point - half_arc
end = mid_point + half_arc
segments.append([start, 1])
segments.append([end, -1])
sorted_segments = sorted(segments, key = lambda x: (x[0], -x[1]))
dart_count = 1
for segment in sorted_segments:
dart_count += segment[1]
ans = max(ans, dart_count)
return ans
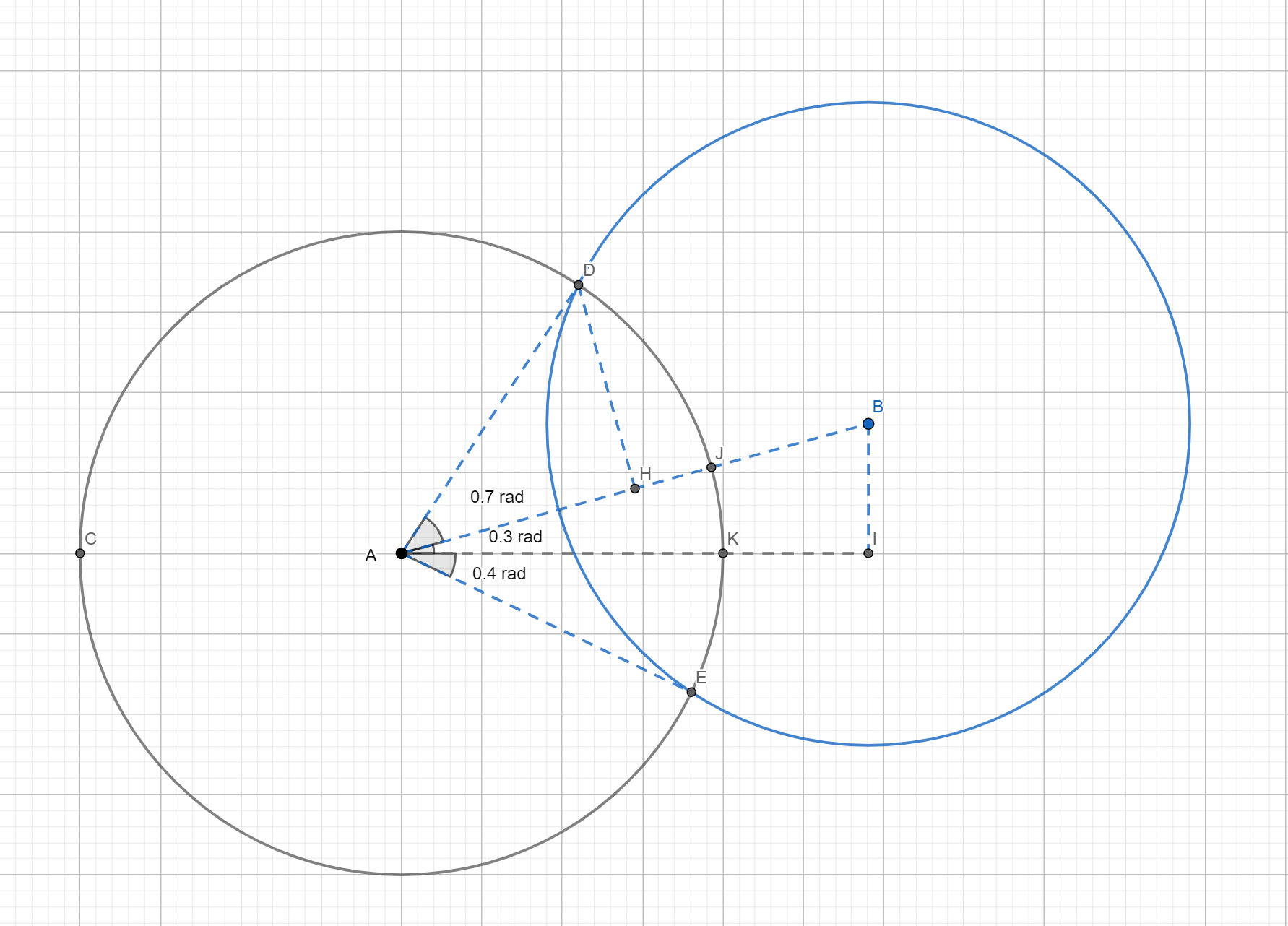
Angle Sweep 2
This is a simlar strategy, instead of drawing points on every dart and calculate overlapping arc. This approach pick a point, and put this point a the circumferance of the circle and measure the enter and exiting angle.
The black angle is very easy to find by taking the arctangen(dy, dx) because P, Q are known points.
The red/blue angle is slightly harder to find. The trick is to realize that triangle PQF is a right angled trangle.
As result will be able to find the angle of either blue or red by taking arccos(|PQ|/2r).
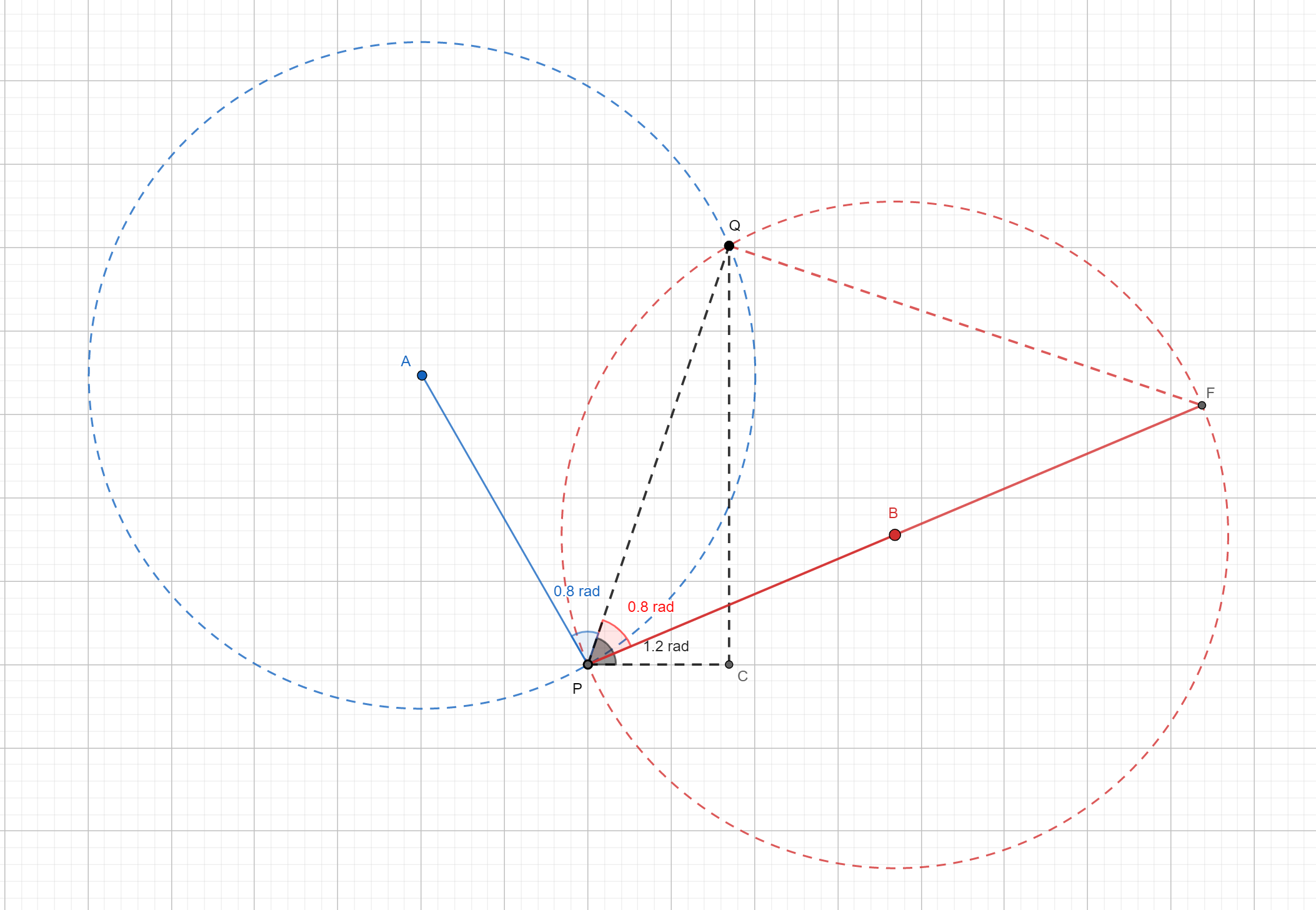
class Solution:
# black angle is `angle`, blue and red is `delta`.
def dist(self, p1, p2):
dx = p1[0] - p2[0]
dy = p1[1] - p2[1]
return math.sqrt(dx ** 2 + dy ** 2)
def numPoints(self, points: List[List[int]], r: int) -> int:
n = len(points)
ans = 1
for i in range(n):
segments = []
for j in range(n):
if i == j:
continue
A, B = points[i], points[j]
if self.dist(A, B) > 2 * r:
continue
delta = acos(self.dist(A, B) / (2 * r))
angle = atan2( (B[1] - A[1]), (B[0] - A[0]) )
segments.append([angle - delta, 1])
segments.append([angle + delta, -1])
sorted_segments = sorted(segments, key = lambda x: (x[0], -x[1]))
# print(sorted_segments)
dart_count = 1
for segment in sorted_segments:
dart_count += segment[1]
ans = max(ans, dart_count)
return ans
What Have I Learned?
What to Keep?
Think of edge case before submitting. All three problems are ACed the first trial. Should keep doing this for future interview sessions.
What not to Do Anymore?
For problem two, I jumped to coding up a custom sorting solution right away. Which turns out to be time wasted because the implementation requires the order of orginal elements keep the same if no need to switch.
I need to think more next time before jump right into coding up the solution.
Author Michael
LastMod 2020-05-17
