Dynamic Programming is Search with Memo
Contents
When preparing for tech interviews, Dynamic Programming(DP) problems are of the most challenging type, in this article we discussed a thinking framework to help solve this type of problem. We also attached a list of actual interview problems with annotated solution as the case study to show how to apply this thiking framework in real scenarios.
DP problems are considered hard mainly because of two reasons.
The first one is the “all or nothing” property of its solutions. Either you found one working state representation and solve the problem fully or you stuck trying. For instance Minimum Cost to Merge Stones is a difficult problem because its state representation is hard to discover.
Another reason is that staring at a working final solution does not reveal any insight on how the solution is derived. For example both solution1 and solution2 solves the above problem. However, looking at the solution itself does not explains how people got there. Sadly often the most upvoted solution does not talk about the thinking proces much.
The remainder of the post presents a thinking framework to help you solve DP problems systematically. This same framework is can also be used to evalute other people’s DP solutions.
Search 101
Let us solve a search problem together to demonstrate the thinking framework.
Minimum Cost Jummping Pillars
Given a list of pillars of different height, player can start at the 0th or 1st position. Everytime the player jump from a pillar, he needs to spend the cost amount equal to the height of the pillar.
What is the minimum cost for the player to jump past all the pillars?
Example 1:
Input: [2, 3, 5, 7, 4]
Output: 10
Explanaiton: Player jupm from pos_1(i.e. 3) then to pos_3(i.e. 7) and finally jump over, total cost is arr[1] + arr[3] = 10.
Example 2:
Input: [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
Output: 6
We want to find out the overall cost, depending on how we jump within limits, the overall cost to arrive at the destination is determined by the pillars we have landed on. If we can examine every single possible path to from one side to the other while keeping track of the minimum cost seen so far duing the enumeration, we will have the answer at the end.
In other words, if we can develop a search strategy to enumerate all the possible paths, we can solve this problem. Of course because we are enumerating all the possbile ways, the time complexity can be large. Another very important thing to notice is that the search strategy you choose is greatly influencing the overal search complexity. (TODO: add concrete example to show one problem can have differnet search strategy with different time complexity) –> Search strategy affects the shape of the search tree.
To examine every possible solution, we need to have an annotation that we can recurse with because computer only knows how to work with mathmatical annotations (i.e. nubmers, and symbols).
If we draw this search process on paper(needs to be animated):
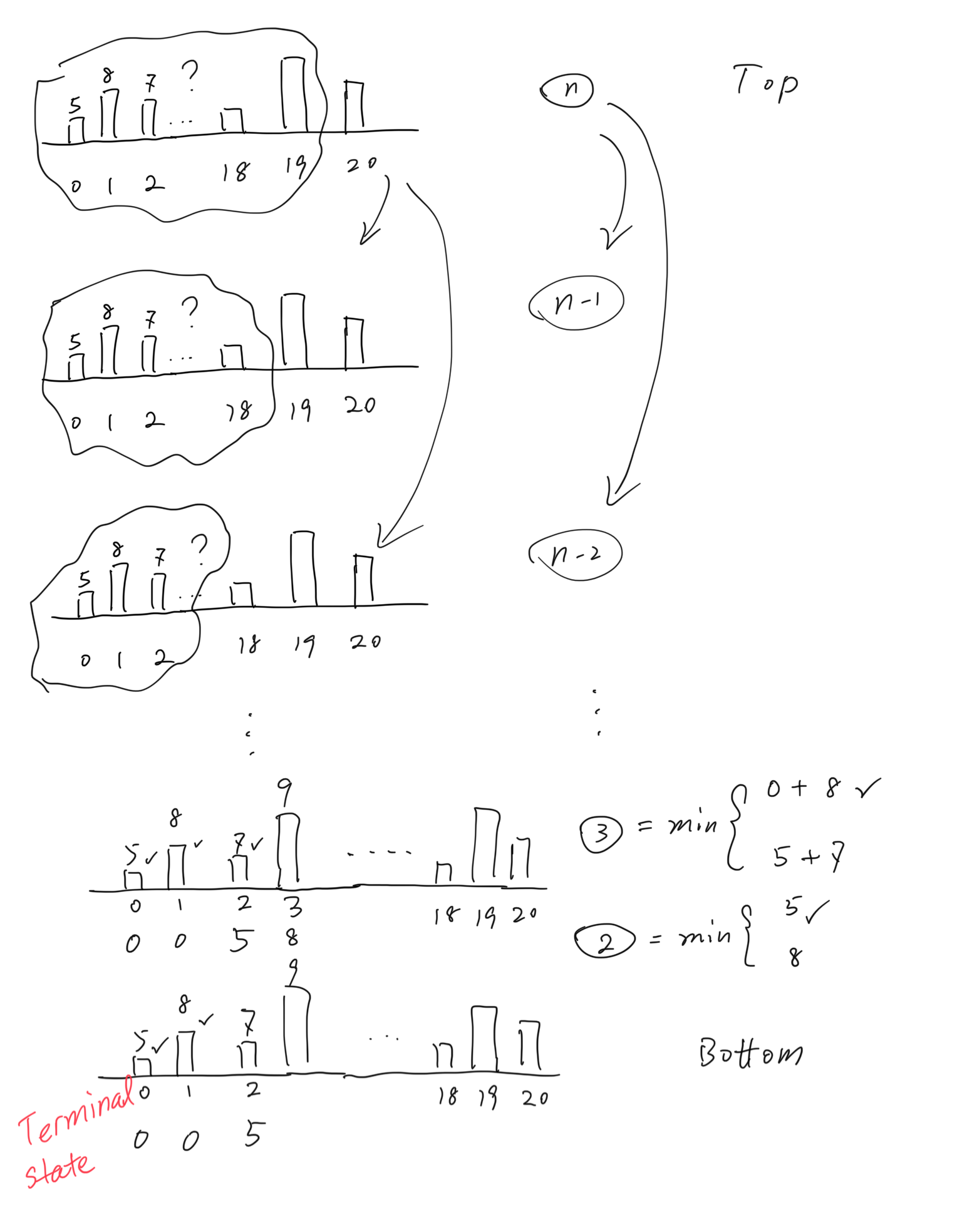
The main problem solving effort is drawing out the recursion tree, especially the part on how to break a node into disjoint sub-nodes. The brach in the search tree represents the choice your search strategy makes at the step.
If you can both draw the recursion tree all the way from root to leaf(base case) and the leaf node is a case that is very easy to solve(can be turned from problem space into answer space). Then you found a succesful recursion strategy. If either you cannot recude the problem into a smaller one or the base case you have arrived cannot be solved directly(turned from problem space into answer space), you will have to try a different search strategy(by searching with more dimension, or make different choices).
After you found a strategy(that is recuding the size, and have easy to solve base cases), your work is already 80% finished. The remainder is just about how to turn this strategy into a representation a computer can understand. You can often do this in two fashions, either a top down fasion where implementation-wise is memorized search or a bottom up fashion where implementation-wise it is induction from base case to bigger and bigger in size.
Issue with most of the problem discussion online is that they skip the answer discovery part(i.e. the drawing on board, the trials and errors of different state representation and recursion startegy). Too many of them start directly with a alredy correct state definition.
After some drawing on board/notebook, you will realize(otherwise you fail to solve this problem) the key information you need to retain at each level of recursion is the position of the pillar the player wants to jump over. To match this observation you obtained from drawing the recussion tree, we can educatively decide that if we create an annotation that captures count of pillar as part of the information in it, we can reduce the problem systematically and eventually reduce it to some easy to solve base case(that can be eye balled).
For this very problem we can finally(with the help of drawing recursion tree out) define our state to be:
notation(n)= total cost player spent to land on pillar n.
Notice that what information you want to capture in state is entirely up to you the problem solver, and mostly come from how you draw out he recursion tree. Therefore this is the step that needs experience (hence varies dramatically from people to people). This is also why there can be more than one working solution to a same searching problem.
Because we want to minimize the overall cost, we need to make such choice at each level. Global min is obtained by collecting all local mins.
notation(n) = min( notation(n-1) + height_n-1, notation(n-2) + height_n-2 )
At this stage, we can write our core logic for the search strategy:
# Step1: Create main recursion logic.
def notation(arr, n):
# ... base case
cnt_level_total_cost = \
min(notation(n - 2) + arr[n - 2], \
notation(n - 1) + arr[n - 1])
return cnt_level_total_cost
This part we just finished is the so called state transition. This is the typically the most logic heavy part of every DP problem. The key operation here is the min. Because our strategy makes a deliverate choice to pick the smaller one at every single recursion level, as the result our top level answer will be the overall minimized cost.
Now with the state transition in place, we will be able to rewrite a bigger sized problem into a smaller sized problem.
We can do this at each recursion level and the problem size will eventualy be so small that solving it becomes very trivial. For instance, of this very problem. We can reduce the problem into base case when we have only the 0th or 1st pillar to land on. For palyer to land on 0th position, notation(0) = 0 because we can start at 0th position. For player to land on 1st position, notation(1) = 0 because player can also start at 1st position. Such process is called base case/initial state. So the code then becomes:
# Step2: Add base case handling.
def notation(arr, n):
if n == 0:
return 0
if n == 1:
return 0
cnt_level_total_cost = \
min(notation(n - 2) + arr[n - 2], \
notation(n - 1) + arr[n - 1])
return cnt_level_total_cost
At this point you have finished a recursive version of the solution.
Notice that during the process of developing a working solution to this problem, we did not mention anything about DP.
The core concepts are all from search. state is a search state, it is a collection of information we want to maintain at each recursion level. state transition is about how to express a big problem state in terms of smaller problem state. Finally base case is the leaf level of recursion tree with witch the recursion can terminate.
So why does this example have anything to do with DP?
Recursion with overlapping sub-problem
As I mentioned before, we are going to discuss why understanding search is important to understanding DP. This is really because DP turns out to be a special kind of search problem. Not every search problem gets to be a DP problem, only those with nice properties do.
In order to qulify as a DP problem, there a search problem needs to have overlapping sub-problems. For our example, problem of size 7 depends on problem of size 6 and size 5. When we want to solve problem of size 6 which in term depends on size 4 and 5. The overlapping subproblem(for problem of size 6 and 7) here is the problem of size 5. Its answer can be reused to solve both problem of size 6 and 7.
If we draw the diagram, it will look like the following:
Notice that a regular search problem does not have overlapping subsubproblem therefore does not qualify as a DP problem because there is no overlapping subproblems to reuse results from, every state needs to be searched, there is no work to be reused.
DP is a technique utilzing table to speed up search
Since DP is just a technique that can be applied to avoid duplicate work when solving problems recursively. The key concepts are from search: state is a search state; state transion is how big problem breaks into smaller ones; finally base case are leaf level of recursion tree.
The very thing that is unique to DP is the table/memo we used in our algorithm to avoid duplicate computation. Overlapping subproblem only needs to be solved once and used many times to construct solution to bigger problems. The answer of each search state can be saved aside and looked up when needed. Such space and computation trade off is core to every DP problem.
When someone fails to solve a DP problem, it is most often due to not being able to solve the underlying search problem, instead of not being able to use a memo to save answer to every search stage. Utilizing memo on top of an already working search strategy is typically the easy part.
As result, when pracitcing, we should spend most of the time thinking about how to break problem down into disjoint subproblems.
For our example search problem that is DP eligible(because of overlapping subproblem), wen can mechnically apply memorization like the following:
# Step 3: Add memo to avoid duplicate computation
def notation(arr, n, memo):
if n in memo:
return memo[n]
if n == 0:
return 0
if n == 1:
return 0
cnt_level_total_cost = \
min(notation(n - 2) + arr[n - 2], \
notation(n - 1) + arr[n - 1])
memo[n] = cnt_level_total_cost
return memo[n]
def jump_cost(arr):
return notation(arr + [0], len(arr))
With the above, we have produced a dynamic programming solution to the problem.
The Thinking Framework
Let’s summarize what we have learned.
- Only those search problems with overlapping subproblems can benefit from DP techinque.
- How to define search state is highly up to each problem solver, this is also why same problem can have very different DP strategy due caused by different state representation.
To systematically tackle this challenge, the following thinking framework will help:
- Define search state for the problem. Think about what is the information needed at each recursion level. Those information becomes your problem state. For example the final index of pillar a player needs to land on.
- Draw out the recursion tree base on your state representation at step 1. If you cannot draw out the recusion tree all the way from root to leaf level. Then either you found the wrong state representation (for instance, miss keeping the complete set of info needed at each recursion level) or you had the right state representation but could not quite make the right decision at each recursion level to successfully reduce the problem into smaller problems.
- Write down the state transition step into code as your main logic.
- Apply memorization to the code.
Out of the four steps, step 2 is the most important step, which should take most of your effort. There may be back and forth between this and the 1st step until you are convinced you can draw out the whole recursion tree. (which would imply that you have both found a working node definition and the correct way to recurse(for instance by taking min operation) into deeper level of recursion tree)
Some useful question you ask yourself for step 2:
What information do I need to capture at each level so I can define the right state? –> state
What choice do I have at current level to make my overall answer globally optimimal? –> state transition
With the above thinking framework, we have successfully handled all three key aspects of every sinlge DP problem.
Top-down vs Bottom-up
These are directions on recursion trees. Top is the start of recursion tree, bottom is the leaf level of recursion tree.
Starting out from a big problem and break it down into smaller ones is called top down. Bottom up means starting out from the base case to build answer up to the original problem.
We can convert the above top down approach to a bottom up one and vise-versa. The only trick here is to start from initial state and compose the answer using already solved sub problme. For this particular example, a bottom up version would be:
# bottom up approach
def jump_cost(arr):
notation = [0] * (len(arr) + 1)
for i in range(2, len(notation)):
notation[i] = min(notation[i - 1] + arr[i - 1], notation[i - 2] + arr[i - 2])
return notation[len(arr)]
Can this be used to solve more difficult problems?
Yes, see in depth discussion on:
- burst balloons
- coin change 1, 2
- backpack problems
Types of Dynamic Programming Problems
From the above example we can conlude that how you defined the search state(), and the search strategy(choices you make) is the core to a dynamic programming problem.
Ther are these common types of dynamic programming problmes. They are different because the state representation and search strategy are different.
- case study for categories of DP problems
- 1D
- 2D
- DP state not directly the answer
- longest fib_like sub-sequence
- longest increasing sub-sequence
- matrix multiplication
Author Michael
LastMod 2020-05-15
